Lecture 9: From dense to sparse linear algebra¶
Recap of the previous lectures¶
- Algorithms for the symmetric eigenvalue (SEV) problem
- QR algorithm with shifts
- Divide-and-Conquer
- bisection
- Jacobi method
- Reduction problem of computing SVD to SEV problem
Interesting fact¶
Before
$$A_k = Q_k R_k, \quad A_{k+1} = R_k Q_k,$$
there was $LU-UL$ algorithm by Heinz Rutishauser
$$A_k = L_k U_k, \quad A_{k+1} = U_k L_k.$$
This generates a sequence of similar matrices, but is less stable than QR algorithm.
Interesting fact: Heinz Rutishauser has proposed the for keyword in programming language. More details about history of for-loop in different languages are available here
Large scale dense matrices¶
- If the size of the dense matrix is huge, then it can not be stored in memory
- Possible options
- This matrix is structured, e.g. block Toeplitz with Toeptitz blocks (next lectures). Then the compressed storage is possible
- For unstructured dense matrices distributed memory helps
- MPI for processing distributed storing matrices
Distributed memory and MPI¶
- Split matrix into blocks and store them on different machines
- Every machine has its own address space and can not damage data on other machines
- In this case machines communicate with each other to aggregate results of computations
MPI (Message Passing Interface) is a standard for parallel computing in distributed memory
Skoltech owns supercomputer, which is on the 6th place in the list of TOP50 supercomputers from Commonwealth of Independent States (see the rating here, sorry for only in Russian)
Example: matrix-by-vector product¶
- Assume you want to compute $Ax$ and matrix $A$ can not be stored in available memory
- Then you can split it on blocks and distribute blocks on separate machines
- Possible strategies
- 1D blocking splits only rows on blocks
- 2D blocking splits both rows and columns
1D blocking scheme¶
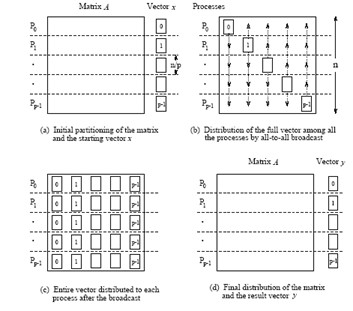
Total time of computing matvec with 1D blocking¶
- Each machine has $n / p $ complete rows and $n / p$ elements of vector
- Total operations are $n^2 / p$
- Total time for sending and writing data are $t_s \log p + t_w n$, where $t_s$ time unit for sending and $t_w$ time unit for writing
2D blocking scheme¶
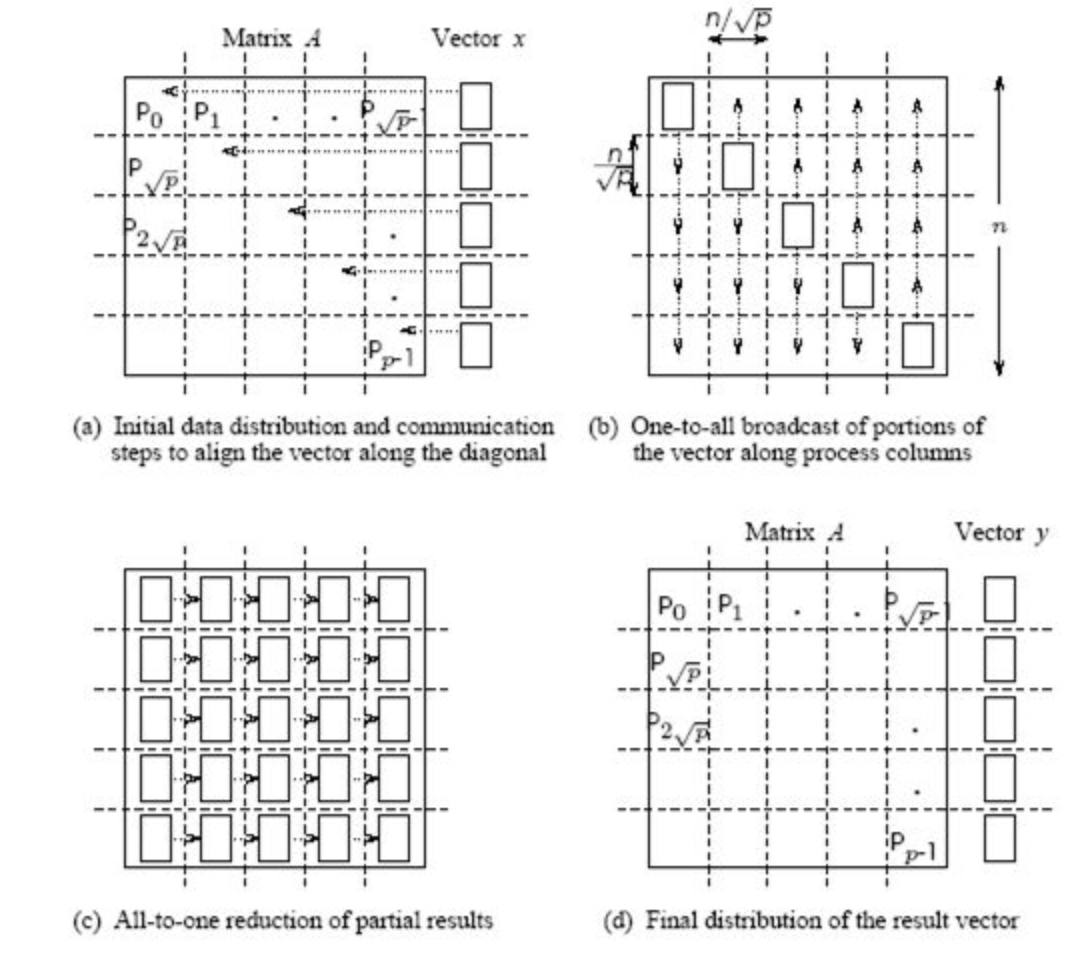
Total time of computing matvec with 2D blocking¶
- Each machine has $n / \sqrt{p} $ size block and $n / \sqrt{p}$ elements of vector
- Total operations are $n^2 / p$
- Total time for sending and writing data are approximately $t_s \log p + t_w (n/\sqrt{p}) \log p$, where $t_s$ time unit for sending and $t_w$ time unit for writing
Summary on large unstructered matrix processing¶
- Distributed manner of storage
- MPI
- Packages that use parallel computrations
- Different blocking strategies
Sparse matrices intro¶
For dense linear algebra problems, we are limited by the memory to store the full matrix, it is $N^2$ parameters.
The class of sparse matrices where most of the elements are zero, allows us at least to store such matrices.
The question if we can:
- solve linear systems
- solve eigenvalue problems
with sparse matrices
Plan for the second part of the lecture¶
Now we will talk about sparse matrices, where they arise, how we store them, how we operate with them.
- Formats: list of lists and compressed sparse row format, relation to graphs
- Matrix-by-vector product
- Parallell processing of sparse matrices
- Fast direct solvers for Gaussian elimination (start)
Applications of sparse matrices¶
Sparse matrices arise in:
- partial differential equations (PDE), mathematical modelling
- graphs mining, e.g. social networks analysis
- recommender systems
- wherever relations between objects are "sparse".
Sparse matrices are ubiquitous in PDE¶
The simplest partial differential equation (PDE), called
Laplace equation:
$$ \Delta T = \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} = f(x,y), \quad x,y\in \Omega\equiv[0,1]^2, $$
$$ T_{\partial\Omega} = 0. $$
Discretization¶
$$\frac{\partial^2 T}{\partial x^2} \approx \frac{T(x+h) + T(x-h) - 2T(x)}{h^2} + \mathcal{O}(h^2),$$
same for $\frac{\partial^2 T}{\partial y^2},$
and we get a linear system.
First, let us consider one-dimensional case:
After the discretization of the one-dimensional Laplace equation with Dirichlet boundary conditions we have
$$\frac{u_{i+1} + u_{i-1} - 2u_i}{h^2} = f_i,\quad i=1,\dots,N-1$$
$$ u_{0} = u_N = 0$$ or in the matrix form
$$ A u = f,$$ and (for $n = 5$) $$A=-\frac{1}{h^2}\begin{bmatrix} 2 & -1 & 0 & 0 & 0\\ -1 & 2 & -1 & 0 &0 \\ 0 & -1 & 2& -1 & 0 \\ 0 & 0 & -1 & 2 &-1\\ 0 & 0 & 0 & -1 & 2 \end{bmatrix}$$
The matrix is triadiagonal and sparse
(and also Toeplitz: all elements on the diagonal are the same)
Block structure in 2D¶
In two dimensions, we get equation of the form
$$-\frac{4u_{ij} -u_{(i-1)j} - u_{(i+1)j} - u_{i(j-1)}-u_{i(j+1)}}{h^2} = f_{ij},$$
or in the Kronecker product form
$$\Delta_{2D} = \Delta_{1D} \otimes I + I \otimes \Delta_{1D},$$
where $\Delta_{1D}$ is a 1D Laplacian, and $\otimes$ is a Kronecker product of matrices.
For matrices $A\in\mathbb{R}^{n\times m}$ and $B\in\mathbb{R}^{l\times k}$ its Kronecker product is defined as a block matrix of the form
$$ A\otimes B = \begin{bmatrix}a_{11}B & \dots & a_{1m}B \\ \vdots & \ddots & \vdots \\ a_{n1}B & \dots & a_{nm}B\end{bmatrix}\in\mathbb{R}^{nl\times mk}. $$
In the block matrix form the 2D-Laplace matrix can be written in the following form:
$$A = -\frac{1}{h^2}\begin{bmatrix} \Delta_1 + 2I & -I & 0 & 0 & 0\\ -I & \Delta_1 + 2I & -I & 0 &0 \\ 0 & -I & \Delta_1 + 2I & -I & 0 \\ 0 & 0 & -I & \Delta_1 + 2I &-I\\ 0 & 0 & 0 & -I & \Delta_1 + 2I \end{bmatrix}$$
Short list of Kronecker product properties¶
- It is bilinear
- $(A\otimes B) (C\otimes D) = AC \otimes BD$
- Let $\mathrm{vec}(X)$ be vectorization of matrix $X$ columnwise. Then $\mathrm{vec}(AXB) = (B^T \otimes A) \mathrm{vec}(X).$
Sparse matrices help in computational graph theory¶
- Graphs are represented with adjacency matrix, which is usually sparse
- Numerical solution of graph theory problems are based on processing of this sparse matrix
- Community detection and graph clustering
- Learning to rank
- Random walks
- Others
- Example: probably the largest publicly available hyperlink graph consists of 3.5 billion web pages and 128 billion hyperlinks, more details see here
- More medium scale graphs to test your algorithms are available in Stanford Large Network Dataset Collection
Florida sparse matrix collection¶
More sparse matrices you can find in Florida sparse matrix collection which contains all sorts of matrices for different applications.
from IPython.display import HTML
HTML('<iframe src=http://yifanhu.net/GALLERY/GRAPHS/search.html width=700 height=450></iframe>')
Sparse matrices and deep learning¶
- DNN has a lot of parameters
- Some of them may be redundant
- How to prune the parameters without significantly accuracy reduction?
- Sparse variational dropout method leads to significantly sparse filters in DNN almost without accuracy decreasing

Sparse matrix: construction¶
We can create sparse matrix using scipy.sparse package (actually this is not the best sparse matrix package)
We can go to really large sizes (at least, to store this matrix in the memory)
Please note the following functions
- Create sparse matrices with given diagonals
spdiags - Kronecker product of sparse matrices
kron - There is also overloaded arithmectics for sparse matrices
import numpy as np
import scipy as sp
import scipy.sparse
from scipy.sparse import csc_matrix, csr_matrix
import matplotlib.pyplot as plt
import scipy.linalg
import scipy.sparse.linalg
%matplotlib inline
n = 5
ex = np.ones(n);
lp1 = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
e = sp.sparse.eye(n)
A = sp.sparse.kron(lp1, e) + sp.sparse.kron(e, lp1)
A = csc_matrix(A)
plt.spy(A, aspect='equal', marker='.', markersize=5)
Sparsity pattern¶
The
spycommand plots the sparsity pattern of the matrix: the $(i, j)$ pixel is drawn, if the corresponding matrix element is non-zero.Sparsity pattern is really important for the understanding the complexity of the sparse linear algebra algorithms.
Often, only the sparsity pattern is needed for the analysis of "how complex" the matrix is.
Sparse matrix: definition¶
The definition of "sparse matrix" is that the number of non-zero elements is much less than the total number of elements.
You can do the basic linear algebra operations (like solving linear systems at the first place) faster, than if working for with the full matrix.
What we need to find out to see how it actually works¶
Question 1: How to store the sparse matrix in memory?
Question 2: How to multiply sparse matrix by vector fast?
Question 3: How to solve linear systems with sparse matrices fast?
Sparse matrix storage¶
There are many storage formats, important ones:
- COO (Coordinate format)
- LIL (Lists of lists)
- CSR (compressed sparse row)
- CSC (compressed sparse column)
- Block variants
In scipy there are constructors for each of these formats, e.g.
scipy.sparse.lil_matrix(A).
Coordinate format (COO)¶
The simplest format is to use coordinate format to represent the sparse matrix as positions and values of non-zero elements.
i, j, val
where i, j are integer array of indices, val is the real array of matrix elements.
So we need to store $3\cdot$ nnz elements, where nnz denotes number of nonzeroes in the matrix.
Q: What is good and what is bad in this format?
Main disadvantages¶
- It is not optimal in storage (why?)
- It is not optimal for matrix-by-vector product (why?)
- It is not optimal for removing elements as you must make nnz operations to find one element (this is good in LIL format)
First two disadvantages are solved by compressed sparse row (CSR) format.
Compressed sparse row (CSR)¶
In the CSR format a matrix is stored as 3 different arrays:
ia, ja, sa
where:
- ia (row start) is an integer array of length $n+1$
- ja (column indices) is an integer array of length nnz
- sa (values) is an real-value array of length nnz

So, we got $2\cdot{\bf nnz} + n+1$ elements.
CSR helps in sparse matrix by vector product (SpMV)¶
for i in range(n):
for k in range(ia[i]:ia[i+1]):
y[i] += sa[k] * x[ja[k]]
Let us do a short timing test
import numpy as np
import scipy as sp
import scipy.sparse
import scipy.sparse.linalg
from scipy.sparse import csc_matrix, csr_matrix, coo_matrix
import matplotlib.pyplot as plt
%matplotlib inline
n = 1000
ex = np.ones(n);
lp1 = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
e = sp.sparse.eye(n)
A = sp.sparse.kron(lp1, e) + sp.sparse.kron(e, lp1)
A = csr_matrix(A)
rhs = np.ones(n * n)
B = coo_matrix(A)
%timeit A.dot(rhs)
%timeit B.dot(rhs)
As you see, CSR is faster, and for more unstructured patterns the gain will be larger.
Sparse matrices and efficiency¶
- Sparse matrices give complexity reduction.
- But they are not very good for parallel/GPU implementation.
- They do not give maximal efficiency due to random data access.
- Typically, peak efficiency of $10\%-15\%$ is considered good.
Recall how we measure efficiency of linear algebra operations¶
The standard way to measure the efficiency of linear algebra operations on a particular computing architecture is to use flops (number of floating point operations per second)
We can measure peak efficiency of an ordinary matrix-by-vector product.
import numpy as np
import time
n = 4000
a = np.random.randn(n, n)
v = np.random.randn(n)
t = time.time()
np.dot(a, v)
t = time.time() - t
print('Time: {0: 3.1e}, Efficiency: {1: 3.1e} Gflops'.\
format(t, ((2 * n ** 2)/t) / 10 ** 9))
n = 400
ex = np.ones(n);
a = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
rhs = np.random.randn(n)
t = time.time()
a.dot(rhs)
t = time.time() - t
print('Time: {0: 3.1e}, Efficiency: {1: 3.1e} Gflops'.\
format(t, (3 * n) / t / 10 ** 9))
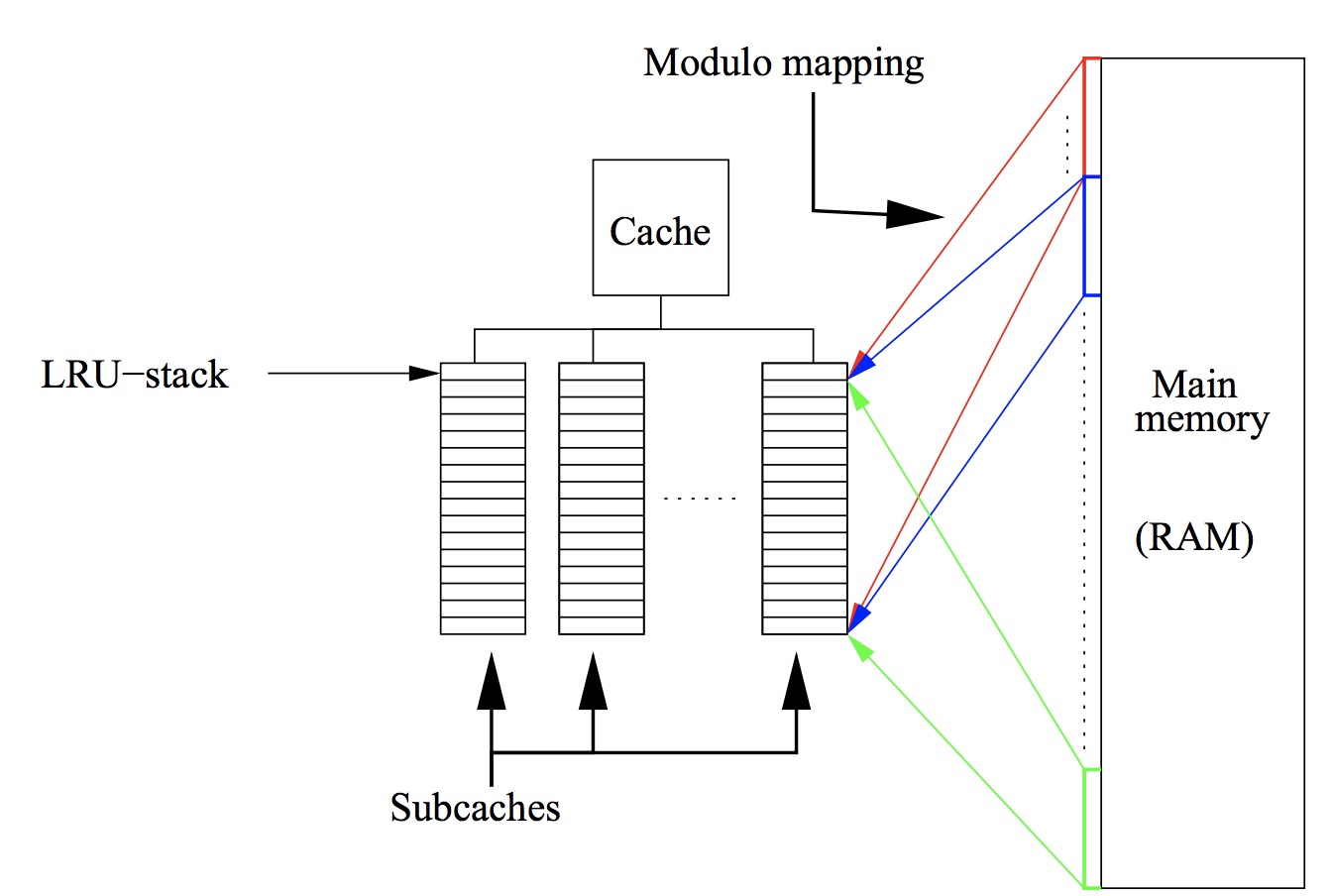
Random data access and cache misses¶
- Initially all matrix and vector entries are stored in RAM (Random Access Memory)
- If you want to compute matvec, the part of matrix and vector elements are moved to cache (fast and small capacity memory, see lecture about Strassen algorithm)
- After that, CPU takes data from cache to proccess it and then returns result in cache, too
- If CPU needs some data that is not already in cache, this situation is called cache miss
- If cache miss happens, the required data is moved from RAM to cache
Q: what if cache does not have free space?
- The larger number of cache misses, the slower computations
Cache scheme and LRU¶
CSR sparse matrix by vector product¶
for i in range(n):
for k in range(ia[i]:ia[i+1]):
y[i] += sa[k] * x[ja[k]]
- What part of operands is strongly led cache misses?
- How this issue can be solved?
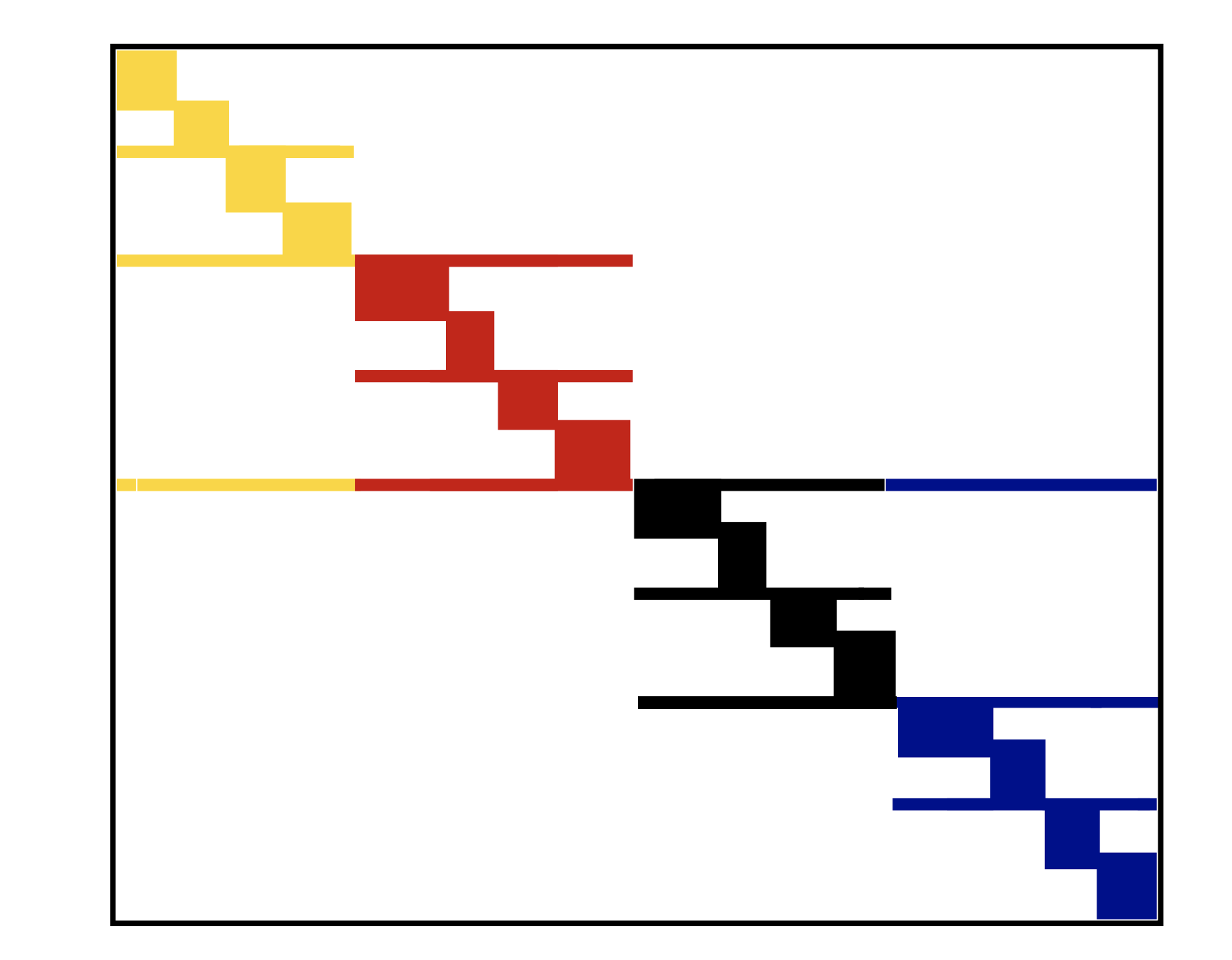
Reordering reduces cache misses¶
- If
jastores sequential elements, then they will be moved to cache altogether and number of cache misses decreases - This happens when sparse matrix is banded or at least block diagonal
We can convert given sparse matrix to banded or block diagonal with permutations
Let $P$ be row permutation matrix and $Q$ be column permutation matrix
- $A_1 = PAQ$ is a matrix, which has less bandwith than $A$
- $y = Ax \to \tilde{y} = A_1 \tilde{x}$, where $\tilde{x} = Q^{\top}x$ and $\tilde{y} = Py$
- Separated block diagonal form is a cache-oblivious format for sparse matrix by vector product
- It can be extended for 2D, where separated not only rows, but also columns
Example¶
- SBD in 1D
Sparse transpose matrix-by-vector product¶
- In some cases it is important to compute not only $Ax$ for sparse $A$, but also $A^{\top}x$
- Mort details will be discussed in the lecture about Krylov methods for non-symmetric linear systems
- Transposing is computationally expensive
- Here is proposed compressed sparse block format of storage appropriate for this case
Compressed sparse block (CSB)¶
- Split matrix in blocks
- Store block indices and indices of data inside each block
- Thus, feasible number of bits to store indices
- Ordering of the blocks and inside blocks is impoprtant for parallel implementation
- Switching between blockrow to blockcolumn makes this format appropriate to transpose matrix by vector product
Solve linear systems with sparse matrices¶
- Direct methods (start today and continue in the next lecture)
- LU decomposition
- Number of reordering techniques to minimize fill-in
- Krylov methods
Let us start with small demo of solving sparse linear system...
n = 10
ex = np.ones(n);
lp1 = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
e = sp.sparse.eye(n)
A = sp.sparse.kron(lp1, e) + sp.sparse.kron(e, lp1)
A = csr_matrix(A)
rhs = np.ones(n * n)
sol = sp.sparse.linalg.spsolve(A, rhs)
_, (ax1, ax2) = plt.subplots(1, 2)
ax1.plot(sol)
ax1.set_title('Not reshaped solution')
ax2.contourf(sol.reshape((n, n), order='f'))
ax2.set_title('Reshaped solution')
Now we start discussion of direct methods for solving sparse linear systems based on LU decomposition...
LU decomposition of sparse matrix¶
Why sparse linear systems can be solved faster, what is the technique?
In the LU factorization of the matrix $A$ the factors $L$ and $U$ can be also sparse:
$$A = L U$$
- And solving linear systems with sparse triangular matrices is very easy.
Note that the inverse matrix is not sparse!
n = 7
ex = np.ones(n);
a = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
b = np.array(np.linalg.inv(a.toarray()))
print(a.toarray())
print(b)
And the factors...¶
$L$ and $U$ are typically sparse. In the tridiagonal case they are even bidiagonal!
from scipy.sparse.linalg import splu
T = splu(a.tocsc(), permc_spec="NATURAL")
print(T.L.toarray())
Interesting to note that splu without permc_spec will produce permutations which will not yield the bidiagonal factor:
from scipy.sparse.linalg import splu
T = splu(a.tocsc())
print(T.L.todense())
print(T.perm_c)
2D-case¶
In a 2D case everything is much worse:
n = 20
ex = np.ones(n);
lp1 = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
e = sp.sparse.eye(n)
A = sp.sparse.kron(lp1, e) + sp.sparse.kron(e, lp1)
A = csc_matrix(A)
T = scipy.sparse.linalg.spilu(A)
plt.spy(T.L, marker='.', color='k', markersize=8)
For correct permutation in 2D case the number of nonzeros in $L$ factor grows as $\mathcal{O}(N \log N)$. But complexity is $\mathcal{O}(N^{3/2})$.
Sparse matrices and graph ordering¶
The number of nonzeros in LU decomposition has a deep connection to the graph theory.
networkx packagecan be used to visualize graphs, given only the adjacency matrix.It may even recover to some extend the graph structure.
import networkx as nx
n = 10
ex = np.ones(n);
lp1 = sp.sparse.spdiags(np.vstack((ex, -2*ex, ex)), [-1, 0, 1], n, n, 'csr');
e = sp.sparse.eye(n)
A = sp.sparse.kron(lp1, e) + sp.sparse.kron(e, lp1)
A = csc_matrix(A)
G = nx.Graph(A)
nx.draw(G, pos=nx.spectral_layout(G), node_size=10)
Fill-in¶
The fill-in of a matrix are those entries which change from an initial zero to a nonzero value during the execution of an algorithm.
The fill-in is different for different permutations. So, before factorization we need to find reordering which produces the smallest fill-in.
Example $$A = \begin{bmatrix}
* & * & * & * & *\\
* & * & 0 & 0 & 0 \\
* & 0 & * & 0 & 0 \\
* & 0 & 0& * & 0 \\
* & 0 & 0& 0 & *
\end{bmatrix}
$$ If we eliminate elements from the top to the bottom, then we will obtain dense matrix. However, we could maintain sparsity if elimination was done from the bottom to the top.
Fill-in minimization¶
Reordering the rows and the columns of the sparse matrix in order to reduce the number of nonzeros in $L$ and $U$ factors is called fill-in minimization.
Examples of algorithms for fill-in minimization:
- Minimum degree ordering - order by the degree of the vertex
- Cuthill–McKee algorithm (and reverse Cuthill-McKee) - reorder to minimize the bandwidth (does not exploit graph representation).
- Nested dissection: split the graph into two with minimal number of vertices on the separator (set of vertices removed after we separate the graph into two distinct connected graphs).
Complexity of the algorithm depends on the size of the graph separator. For 1D Laplacian separator contains only 1 vertex, in 2D - $\sqrt{N}$ vertices.
Take home message¶
- CSR format for storage
- Cache and parallel issues in sparse matrix processing
- Reordering and blocking as a way to solve these issues
- Sparse matrices & graphs ordering
- Ordering is important for LU fill-in: more details in the next lecture